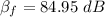Answer:
The value is
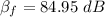
Step-by-step explanation:
From the question we are told that
The intensity level of the shout of a single person is
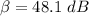
The number of fans is
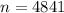
Gnerally intensity level is mathematically represented as

Here
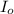 is the minimum intensity of sound human ear can pick and the value is
is the minimum intensity of sound human ear can pick and the value is
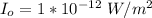
when
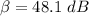

=>
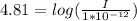
taking antilog of both sides
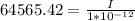
=>
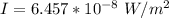
Generally the intensity for the whole fans is mathematically represented as
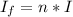
=>

=>
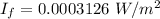
Gnerally the intensity level for the whole fans is mathematically represented as
![\beta_f = 10 log [ (I_f )/(I_o ) ]](https://img.qammunity.org/2021/formulas/physics/college/nuo4vhyir99ke8blfn7rvk70nxy1u249ha.png)
=>
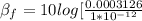
=>