Question

DRaw the graph of f (x) = 1/2 x² -2x where -2 < x < 4​

Answer 1

Graphs Attached Below

Explanation:

Hello!

Standard form of a quadratic:
`ax^2 + bx + c= 0`

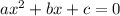
From our Equation:

• a = 1/2
• b = -2
• c = 0

There are several values that are needed to drawing a parabola:

• y - intercept
• Axis of Symmetry (AOS)
• Vertex
• x - intercepts

Y-intercept

Standard form of a quadratic:
`ax^2 + bx + c= 0`

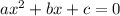
The y-intercept is the "c" value. Given that our equation has a "c" value of 0, the y -intercept is 0.

Axis of Symmetry

A parabola is always symmetrical vertically. The line in which the fold happens is the Axis of Symmetry.

To calculate the AOS, we use the formula
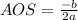`AOS = (-b)/(2a)`, from the values of the equation.

Calculate

• 
  `AOS = (-b)/(2a)`
• 
  `AOS = (-(-2))/(2(0.5))`
• 
  `AOS = (2)/(1)`
• 
  `AOS = 2`

The Axis of Symmetry is a vertical line, so the AOS is the line x = 2.

Vertex

The vertex is the highest or lowest point on the graph of a parabola. It resides on the AOS of the graph.

To calculate the vertex, we simply have to find the y-value, given that we have the x-value from the AOS. We can find the y-value by plugging in the AOS for x in the original equation.

Calculate

• 
  `f(x) = \frac12x^2 - 2x`
• 
  `f(x) = \frac12 (2)^2 - 2(2)`
• 
  `f(x) = 2 - 4`
• 
  `f(x) = -2`

The y-value is -2. The vertex is (2, -2).

X-intercepts

The x-intercepts are the points where the graph intersects the x-axis (y = 0).

Solve by Factoring

• 
  `f(x) = \frac12 x^2 - 2x`
• 
  `0 = \frac12x(x - 4)`
• 
  `x = 0, x = 4`

The roots are (0,0) and (4,0).

Graph

Now we just draw the y-intercept, vertex, AOS, and the x-intercepts, and draw a curved line between them.

Image Attached

Domain Restrictions

The Domain (x-values) are being restricted to all x-values that are greater than or equal to -2 and less than 4.

That means we remove the parts of the line that don't belong in that domain.

Image Attached