Question

Sales personnel for Skillings Distributors submit weekly reports listing the customer contacts made during the week. A sample of 35 weekly reports showed a sample mean of 19.5 customer contacts per week. The population standard deviation was 5.2. Provide a 99% confidence interval for the population mean number of weekly customer contacts for the sales personnel.

Answer 1

The answer is below

Explanation:

Given that:

Confidence interval (C) = 99%, mean (μ) = 19.5, standard deviation (σ) = 5.2, sample size (n) = 35

α = 1 - C = 1 - 0.99 = 0.01

α/2 = 0.005

The z score of α/2 (0.005) is the same as the z score 0.495 (0.5 - 0.005) which is equal to 2.576.

The margin of error (E) is given as:

`E=Z_(\alpha)/(2)*(\sigma)/(√(n) ) \\\\E=2.576*(5.2)/(√(35) ) \\\\E=2.264`

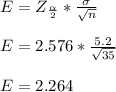
The confidence interval = (μ ± E) = (19.5 ± 2.264) = (17.236, 21.764).

The confidence interval is between 17.236 and 21.764.