Question

Given that (ax^2 + bx + 3) (x+d) = x^3 + 6x^2 + 11x + 12, it asks a + 2b - d = ?

Answer 1

a+2b-d=1, 3, 5, 7

Explanation:

(ax^2+bx+3)(x+d)

ax^3+bx^2+3x+adx^2+bdx+3d

ax^3+bx^2+adx^2+3x+bdx+3d=x^3+6x^2+11x+12

ax^3=x^3, a=1

bx^2+adx^2=6x^2

x^2(b+ad)=6x^2

b+ad=6

b+(1)d=6

b+d=6

------------

3x+bdx=11x

x(3+bd)=11x

3+bd=11

-----------------

b=6-d

3+(6-d)d=11

3+6d-d^2=11

3-11+6d-d^2=0

-8+6d-d^2=0

d^2-6d+8=0

factor out,

(d-4)(d-2)=0

zero property,

d-4=0, d-2=0

d=0+4=4,

d=0+2=2

b=6-4=2,

b=6-2=4.

------------------

a+2b-d=1+2(2)-2=1+4-2=5-2=3

-------------------

a+2(4)-4=1+8-4=9-4=5

-----------------------

a+2(2)-4=1+4-4=5-4=1

-----------------------

a+2(4)-2=1+8-2=9-2=7

Answer 2

`a+2b-d=1`

Explanation:

We are given that:

`(ax^2+bx+3)(x+d)=x^3+6x^2+11x+12`

And we want to determine:

`a+2b-d`

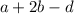
So, we will determine our unknowns first.

We can distribute our expression:

`=(ax^2+bx+3)x+(ax^2+bx+3)d`

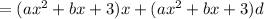
Distribute:

`=ax^3+bx^2+3x+adx^2+bdx+3d`

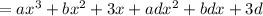
Rearranging gives:

`=(ax^3)+(bx^2+adx^2)+(bdx+3x)+3d`

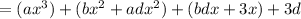
Factoring out the variable yields:

`=(a)x^3+(b+ad)x^2+(bd+3)x+d(3)`

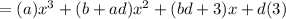
Since we know that our expression equals:

`x^3+6x^2+11x+12`

This means that each of the unknown terms in front of each variable corresponds with the coefficient of the resulting equation. Therefore:

`\begin{aligned} a&=1\\ b+ad&=6\\bd+3&=11\\3d&=12\end{aligned}`

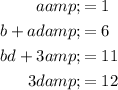
Solving the first and fourth equation yields that:

`a=1\text{ and } d=4`

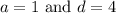
Then the second and third equations become:

`b+(1)(4)=6\text{ and } b(4)+3=11`

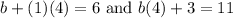
And solving for b now yields that:

`b=2\stackrel{\checkmark}{=}2`

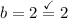
Therefore, we know that:

`a=1, b=2\text{ and } d=4`

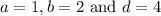
For the equation:

`(x^2+2x+3)(x+4)=x^3+6x^2+11x+ 12`

Then the expression:

`a+2b-d`

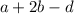
Can be evaluated as:

`=(1)+2(2)-4`

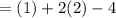
Evaluate:

`=1+4-4=1`

Hence, our final answer is 1.