Question

You are stuck at the Vince Lombardi rest stop on the New Jersey Turnpike with a dead battery. To get on the road again, you need to find someone with jumper cables that connect the batteries of two cars together so you can start your car again. Suppose that 16% of drivers in New Jersey carry jumper cables in their trunk. You begin to ask random people getting out of their cars if they have jumper cables. Use Scenario 6-17. On average, how many people do you expect you will have to ask before you find someone with jumper cables

Answer 1

The expected number of people you will have to ask before you find someone with jumper cables is 6.25.

Explanation:

• The geometric distribution is the distribution of the number of X Bernoulli trials required for one success. If the one success requires k independent trials, each with the probability of success as p, then the probability that the kth trial is the one success is:

`p_(X)(k)=(1-p)^(k-1)p;\ k={1, 2, 3...}`

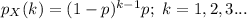
• The geometric distribution is the distribution of the number of Y = X – 1 failures required before the first success. If the first success requires k failures, each trial with the probability of success as p, then the probability that the 1st success occurs after k failures is:

`p_(X)(k)=(1-p)^(k)p;\ k={0, 1, 2, 3...}`

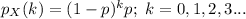
In this case the first scenario follows.

X = number of people you will have to ask before you find someone with jumper cables.

p = 0.16

Compute the expected number of people you will have to ask before you find someone with jumper cables as follows:

`E(X)=(1)/(p)\\\\=(1)/(0.16)\\\\=6.25`

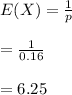
Thus, the expected number of people you will have to ask before you find someone with jumper cables is 6.25.