Question

I can't understand this one bit

Answer 1

It would be $1,590.75 more if it were compounded quarterly than monthly.

Explanation:

In order to solve this problem, you need to understand the Compound Interest Formula.

`A= P(1 + (r)/(n))^t`

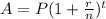
Where A is the Amount, P is the principal or the initial amount received, r is the rate, n is the number of times (per year) it is compounded, and t is the time in years.

The question gives you all of the information to input into the formula. You have the principal, $5000, the rate, 6% (.06), it's being compounded monthly (12 & 4 per year), and we have the years, 25.

We need to compare the two formulas where the only thing that will change is n. n will be 12 (compounded monthly) and 4 (compounded quarterly).

Compounded monthly

`A=5000(1+(0.06)/(12))^(25)\\A = 5663.98`

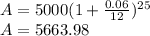
Compounded monthly, the account would have $5,663.98 or $5,664 (simplified).

Compounded quarterly

`A=5000(1+(0.06)/(4))^(25)\\A =7254.73`

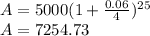
Compounded quarterly, the account would have $7,254.73 or $7,255 (simplified).

Now, we need to find the difference between monthly and quarterly.

7254.73 - 5663.98 = $1,590.75

It would be $1,590.75 more if it were compounded quarterly than monthly.