Question

What is the correct answer?

Answer 1

Option (3)

Step-by-step explanation:

From the graph attached,

Zeros of the function are, x = -3,

Graph of the polynomial touches x axis at x = -3, 1 and 3

Therefore, equation of the given function will be in the form of,

P(x) =
`k(x+3)^a(x-1)^b(x-3)^c`

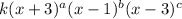
Since, graph of the function just touches the x-axis, multiplicity of zero at x = -3 will be even and crosses x-axis so the multiplicity at x = 1 and 3 will be odd.

Therefore, possible function will be,

P(x) =
`k(x+3)^2(x-1)(x-3)`

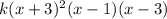
Since, y-intercept of the function is at (0, -3),

P(0) = k(0 + 3)²(0 - 1)(0 - 3)

-3 = 27k

k =
`-(3)/(27)=-(1)/(9)`

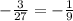
Therefore, given polynomial function is,

P(x) =
`-(1)/(9)(x+3)^(2)(x-1)(x-3)`

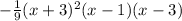
Option (3) will be the correct option.