Question

If x is a positive integer, what is the value of x for the equation (x!-(x-3)!)\23=1?

I think the first step is knowing (x!-(x-3)!) equals to 23, but after that i'm stuck, can someone help me?

Answer 1

`(x!-(x-3)!)/(23)=1\\x!-(x-3)!=23\\(x-3)!((x-2)(x-1)x-1)=23\\(x-3)!((x^3-x^2-2x^2+2x)-1)=23\\(x-3)!((x^3-3x^2+2x)-1)=23`

23 is a prime number, therefore there are two possibilities:

`\text{I.}\, (x-3)!=1 \wedge x^3-3x^2+2x-1=23`

or

`\text{II.}\, (x-3)!=23 \wedge x^3-3x^2+2x-1=1`

`\text{I.}\\(x-3)!=1\\x-3=0 \vee x-3=1\\x=3 \vee x=4`

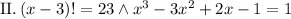
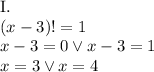
Now, we check if any of these solutions is also a solution to the second equation:

`3^3-3\cdot3^2+2\cdot3-1=23\\27-27+6-1-23=0\\ -18=0`

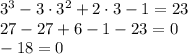
Therefore, 3 is not a solution.

`4^3-3\cdot4^2+2\cdot4-1=23\\64-48+8-1-23=0\\0=0`

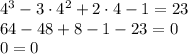
Therefore, 4 is a solution.

`\text{II.}`

`(x-3)!=23`

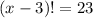
We know that
`3!=6` and
`4!=24`, therefore there isn't any
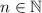`n\in\mathbb{N}`, for which
`n!=23`, so there's no solution.

So, the only solution is
`x=4`.