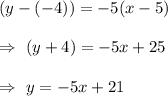Question

Write an equation in slope-intercepts form for the line that passes through (5, -4) and is perpendicular to the line described by 2x-10y=0

EXPLAIN what you did in each step to arrive at your answer plz

Answer 1

Answer:
`y=-5x+21`

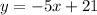
Explanation:

In slope intercept form : y=mx+c , m= slope , c= y-intercept.

Let
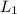`L_1` be the line passing through (5, -4) and perpendicular to
`L_2: 2x-10y=0`.

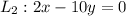Rewrite
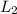`L_2` in slope-intercept form

`10y=2x\Rightarrow\ y=0.2x+0`

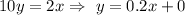
Here, Slope of
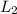`L_2` = m = 0.2

Let n be slope of
`L_1` .

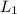Then
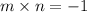`m* n=-1` [Product of slopes of perpendicular lines is -1.]

`\Rightarrow\ n=(-1)/(m)=(-1)/(0.2)\\\\\Rightarrow\ n=-5`

Equation of a line that passes through (a,b) and have slope 'm' is given by :-

`(y-b)=m(x-a)`

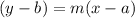
So, Equation of
`L_1` :

`(y-(-4))=-5(x-5)\\\\\Rightarrow\ (y+4)=-5x+25\\\\\Rightarrow\ y=-5x+21`