Question

In AWXY, X = 1.2 cm, ZX=45° and Y=108°. Find the length of w, to the nearest 10th

Answer 1

The length of w is 0.8 cm

Explanation:

In Δ WXY

x is the opposite side to ∠X

w is the opposite side to ∠W

y is the opposite side to ∠Y

∵ m∠X = 45°

∵ m∠Y = 108

∵ The sum of the measures of the interior angle of a triangle is 180°

∴ 45 + 108 + m∠W = 180

→ Add the like terms in the left side

∵ 153 + m∠W = 180

→ Subtract 153 from both sides

∴ m∠W = 27°

Now we can use the sine rule to find the length of w

∵
`(w)/(sin(W))` =
`(x)/(sin(X))` =
`(y)/(sin(Y))`

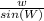→ Use the first 2 ratios to find w

∵ x = 1.2 cm

∵
`(w)/(sin(27))` =
`(1.2)/(sin(45))`

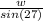→ By using cross multiplication

∴ w × sin(45) = 1.2 × sin(27)

∴ w sin(45) = 1.2 sin(27)

→ Divide both sides by sin(45)

∴ w = 0.7704474263

→ Round it to the nearest tenth

∴ w = 0.8 cm

∴ The length of w is 0.8 cm