Question

A tourist stands at the top of the Grand Canyon, holding a rock, overlooking the valley below. Find the final velocity, and displacement of the rock after 4.0 seconds give the three initial conditions listed below.

a. The rock is dropped vertically from rest
b. The rock is tossed vertically upward with 8.0 m/s of speed
c. The rock is tossed vertically downward with 8.0 m/s of speed TV TV

Answer 1

a. Vf = 39.24 [m/s]

b. Vf = 31.24 [m/s]

c. Vf = 47.24 [m/s].

Step-by-step explanation:

To solve this problem we can use the following equation of kinematics. We have to keep in mind that the gravitational acceleration acts downwards, therefore when the rock falls towards the abyss it has the same direction of the acceleration and that is why the gravitational acceleration has a positive sign in the equation.

`v_(f)=v_(o)+g*t`

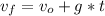
where:

Vf = final velocity [m/s]

Vo = initial velocity = 0 (when the rock is dropped)

g = gravitational acceleration = 9.81 [m/s²]

t = time = 4 [s]

a.

`v_(f)=0+9.81*4\\v_(f)= 39.24 [m/s]`

b.

In this particular situation, the acceleration will be taken as negative because the gravity is pointing in the opposite direction of the movement of the rock.

`v_(f)=8-(9.81*4)\\v_(f)=-31.24[m/s]`

The negative sign in the answer tells us that the rock no longer moves up instead it does downwards when 4 seconds have passed.

c.

`v_(f)=8+(9.81*4)\\v_(f)=47.24[m/s]`