Question

In △ABC, AB = 13.2m, BC = 6.9m and ∠ACB = 90°. H lies on AC such that ∠BHC = 46°. Find (i) ∠ABH (ii) The length of AH

Answer 1

(i) ∠ABH = 14.46⁰

(ii) The length of AH = 4.6 m

Explanation:

From the image uploaded;

Consider △ABC;

the length of b is calculated by applying Pythagoras theorem as follows;

b² = c² - a²

b² = (13.2)² - (6.9)²

b² = 126.63

b = √126.63

b = 11.25 m

Also, ∠ABC is calculated as;

`Cos \ B = (a^2+c^2-b^2)/(2ac) \\\\Cos \ B = ((6.9)^2+(13.2)^2-(11.25)^2)/(2(6.9 *13.2))\\\\ Cos \ B = (95.288)/(182.16) \\\\ Cos \ B = 0.5219 \\\\B = Cos ^(-1) (0.5231)\\\\B = 58.46 ^o`

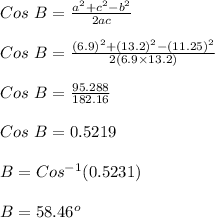
Consider △CBH, ∠CBH is calculated as;

∠CBH = 90⁰ - 46⁰ = 44⁰

(i) ∠ABH will be calculated as;

∠ABH = θ

θ + 44⁰ = ∠ABC

θ + 44⁰ = 58.46⁰

θ = 58.46⁰ - 44⁰

θ = 14.46⁰

Thus, ∠ABH = 14.46⁰

(ii) The length of AH

length HC is calculated as;

`tan \ 46^o =(6.9)/(HC) \\\\HC = (6.9)/(tan \ 46^o ) \\\\HC = 6.66 \ m`

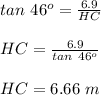
length of AH = CA - HC

x = b - HC

x = 11.25 - 6.66

x = 4.6 m

length of AH = 4.6 m