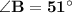The angles of a triangle are described as follows: Angle A is the largest angle; it's measure is twice the measure of Angle B. The measure of Angle C is 10 more than one-th…

Question

asked Feb 4, 2021 167k views

1 Answer

Vvo · Answer 1 · 2021-02-08T21:49:20+0000

Answer:

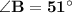
$\bold{\angle B = 51^\circ}$

Explanation:

Given a
$\triangle ABC$ such that
$\angle A$ is the largest.

$\angle A$ is equal twice of
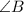
$\angle B$

$\angle C$ is 10 more than one third of
$\angle B$

To find:

Measurement of
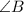$\angle B$ .

Solution:

Let
$\angle B =x^\circ$

As per question statement:

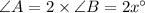
$\angle A = 2* \angle B=2x^\circ$

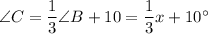
$\angle C = (1)/(3)\angle B +10= (1)/(3)x +10 ^\circ$

Using the angle sum property of a triangle i.e. sum of all the three internal angles is equal to
$180^\circ$ .

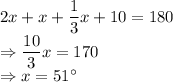
$2x+x+(1)/(3)x+10 = 180\\\Rightarrow (10)/(3)x =170\\\Rightarrow x = 51^\circ$

Therefore, the answer is:

$\bold{\angle B = 51^\circ}$