Question

Find the values of w, x and y.

Answer 1

w= 27.47 degree

x=9.99 cm

y=12.02 cm

Explanation:

The value of w:

In a right-angled triangle
`\tan \theta = \frac {\text{Perpendicular}}{\text{Base}}`

`\tan w = \frac {\text{Perpendicular}}{25+9}\;and \; \tan 63 = \frac {\text{Perpendicular}}{9}`

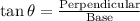
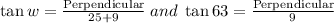
So,
`34 \tan w = 9\tan (63)`

`\tan w = (9/34)\tan(63)=0.52 \\\\w=\tan^(-1)(0.52) \\\\`

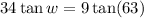
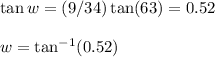
w= 27.47 degree

The value of x:

In a right-angled triangle
`\sin \theta = \frac {\text{Perpendicular}}{\text{Hypotaneous}}`

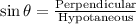
sin (27) =x/22

x= 22sin(27)

x=9.99 cm

The value of y:

By using Pythagoras theorem,

`y^2+y^2=17^2 \\\\2y^2 = 289 \\\\y^2 =289/2= 144.5 \\\\y=\sqrt {144.5} \\\\`

y=12.02 cm