Question

a tiger moving with constant accleration covers the distance between two points 70 meter apart in 7 seconds . its speed as it pass the second point 15 meter per second . 1) what is the speed at the first point. 2) what us its accleration​

Answer 1

a = 1.428 [m/s²]

v₀ = 5 [m/s]

Step-by-step explanation:

To solve this problem we must use the following equation of kinematics.

`x=x_(o)+v_(o)*t+(1)/(2)*a*t^(2)`

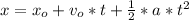
where:

x = final point [m]

x₀ = initial point [m]

v₀ = initial velocity [m/s]

a = acceleration [m/s²]

t = time [s]

But we need to use this additional equation.

`v_(f)=v_(o)+a*t`

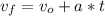
where:

vf = final velocity = 15 [m/s]

Now we can use this equation, replacing it, in the first one. We must bear in mind that the difference among x - x₀ is equal to 70 [m]

`x-x_(o)=v_(o)*t+(1)/(2)*a*t^(2) \\x-x_(o)=(v_(f)-a*t)*t+(1)/(2) *a*t^(2)\\70=(15-a*t)*t+(1)/(2)*a*t^(2)\\70=15*t-a*t^(2) +(1)/(2)*a*t^(2) \\70=15*t-(1)/(2)*a*t^(2)\\70=15*(7)-(1)/(2) *a*(7)^(2)\\105-70=0.5*a*49\\35=24.5*a\\a=1.428[m/s^(2) ]`

Now replacing this value in the second equation, we can find the initial velocity.

`15=v_(o)+1.428*7\\v_(o)=5[m/s]`