Question

(1 pt

Find a formula for P = f(t), the size of the population that begins in year t=0 with 2140 members and decreases at a 3.8% annual rate. Assume
that time is measured in years

Answer 1

The formula f(t) will be:

`\:f\left(t\right)=2150\left(0.962\right)^t`

Explanation:

We know that exponential decline in Maths can be termed as a consistent reduction of an amount by percentage over a certain period of time.

It can be expressed using the formula

`f\left(t\right)=\:a\:\left(1-b\right)^t`

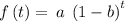
here

f(t) represents the final amount

a represents the original amount

b represents the decay factor

t represents the amount that has passed

Now, map our problem using the same concept formula

as

2150 members are at the beginning, so

a = 2150

as the size of the population has been experiencing an annual decline of 3.8%. so

b = 3.8%= 0.038

so substituting b = 0.038 and a = 2150

`P=f\left(t\right)=\:a\:\left(1-b\right)^t`

`\:f\left(t\right)=2150\left(1-0.038\right)^t`

`\:f\left(t\right)=2150\left(0.962\right)^t`

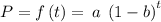
Therefore, the formula f(t) will be:

`\:f\left(t\right)=2150\left(0.962\right)^t`