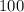Answer:
The correct answer is "100".
Step-by-step explanation:
The given values are:
X (mean) = 5
X (standard deviation) = 25
Variance of X will be:
=

=
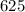
The solution of the part first is:
The given equation is :
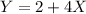
On putting the value of x in above equation we get ,
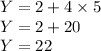
So we get the mean of Y is 22
For finding the S.D of Y
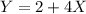
So,
variance of Y= Var(2+4X)
As we know that the variance of constant is zero
So, variance (2) =0
⇒

⇒
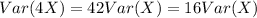
So,
⇒
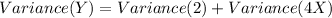
We know the variance of constant is zero
So, var(2)=0
⇒

Thus the standard deviation of Y is:
=

=