Question

A football tube in the form of a sphere is inflated so that it radius increases in the ratio 4:3 . Find the ratio in which the volume is increased. ​

Answer 1

The volume is increased in a ratio of 64/27

Step-by-step explanation:

The Volume of a Sphere

The volume of a sphere of radius r is given by:

`\displaystyle V=(4)/(3)\cdot \pi\cdot r^3`

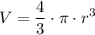
If the radius was changed to r', the new volume would be:

`\displaystyle V'=(4)/(3)\cdot \pi\cdot r'^3`

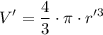
Dividing the latter equation by the first one:

`\displaystyle (V')/(V)=((4)/(3)\cdot \pi\cdot r'^3)/((4)/(3)\cdot \pi\cdot r^3)`

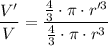
Simplifying:

`\displaystyle (V')/(V)=(r'^3)/(r^3)`

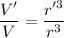
Or, equivalently:

`\displaystyle (V')/(V)=\left((r')/(r)\right)^3`

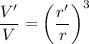
Since r':r = 4:3, thus:

`\displaystyle (V')/(V)=\left((4)/(3)\right)^3`

`\displaystyle (V')/(V)=(4^3)/(3^3)`

`\displaystyle (V')/(V)=(64)/(27)`

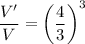
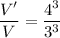
The volume is increased in a ratio of 64/27