Question

I. Is point (6;-2) solution for -4x-5y=32? Why? Show me the steps how are checking?

II. What is the slope of the line through (-4,1) and (-7,-5)? Write the formula and show me the
solution.

III. What is the slope of the line x=-7? Why?

IV. What is the slope of the line y=-6? Why?

V. What will be x and y intercepts for the given equation y= -2x+25? How will you find them?

VI. Write the equation of the line through (-3,8) and (-4,-9) points.​

Answer 1

I. The point (6, -2) is not a solution for the given equation

II. The slope of the line going through (-4, 1) and (-7, -5) is 2

III. The slope of the line x = -7 is ∞

IV The slope of the line y = -6 is 0

V. The coordinate of the x-intercept is (12.5, 0)

The coordinate of the y-intercept is (0, 25)

VI. The equation of the line is y = 17·x + 59

Explanation:

I. The given equation is -4·x - 5·y = 32

The given point = (6, -2)

Therefore;

The x-coordinate value of the point = 6

The y-coordinate value of the point = -2

Plugging in the x and y-coordinate values into the given equation gives;

-4 × (6) - 5 × (-2) = -14 which does not correspond to the given equation, therefore, the point (6, -2) is not a solution for the given equation;

We can also show, by making y the subject of the formula of the given equation, weather the point is a solution of the given equation as follows;

-4·x - 5·y = 32

y = (-4/5)·x - 32/5

For x = -2, we have;

y = (-4/5) × (-2) - 32/5 = - 4.8

Therefore, the point (6, -2) where y = 6 when x = -2 is not a solution of -4·x - 5·y = 32

II. The slope of a straight line, given two points on the line is given as follows;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

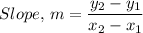
Where the two points are (-4, 1), and (-7, -5), we have;

x₁ = -4, y₁ = 1, x₂ = -7, and y₂ = -5

`Slope, \, m =(-5-1)/(-7-(-4)) =2`

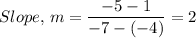
The slope, m, of the line going through (-4, 1) and (-7, -5) is m = 2

III. The slope of the line x = -7 = ∞ because, the difference in the x-value which is the denominator of the slope equation = 0 for all differences in the y-coordinate values

IV The slope of the line y = -6 is 0 because, the difference in the y-values which is the numerator of the slope equation = 0 for all differences in the x-coordinate values

V. The x and y-intercept of an equation is found by finding the values of the variable, x or y, in the equation, when the other variable, y or x is equal to zero respectively, which is given as follows;

The given equation is y = -2·x + 25

When y = 0, we have the x-intercept as 0 = -2·x + 25

∴ 2·x = 25

x = 25/2 = 12.5

Therefore, the coordinate of the x-intercept is (12.5, 0)

When x = 0, we have the x-intercept as y = -2·x + 25 = -2 × 0 + 25 = 25

The coordinate of the y-intercept is (0, 25)

VI. The general equation of a straight line is y = m·x + c

Where;

m = The slope of the line

c = The y-intercept

For the line that goes through the points (-3, 8) and (-4, -9), we have;

`The \ slope, \, m =(-9-8)/(-4- (-3)) = (-9-8)/(-4+3) = 17`

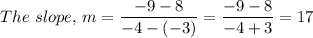
The equation in point and slope form is y - 8 = 17 × (x - (-3))

∴ y = 17·x + 51 + 8 = 17·x + 59

The equation of the line is y = 17·x + 59