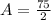Answer:
the area of the curve y= f(x) = x between x = 5 and x = 10
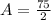
Explanation:
- Finding the area of the curve y = f(x) = x between x = 5 and x = 10
Using the Area formula
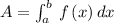
As the area of curve lies between x = 5 and x = 10
so
so the integral expression becomes
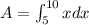
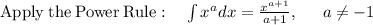
![A=\left[(x^(1+1))/(1+1)\right]^(10)_5](https://img.qammunity.org/2021/formulas/mathematics/college/x1h0bqob2en8arnm9a88uo9m1qlhiiafnf.png)
![=\left[(x^2)/(2)\right]^(10)_5](https://img.qammunity.org/2021/formulas/mathematics/college/ktkvr7esm65ljsoxx8d6dzy1j84mbaj7wq.png)
![=(1)/(2)\left[10^2-5^2\right]](https://img.qammunity.org/2021/formulas/mathematics/college/n5b131kf9uagysj28p02evga2g5lp5kzki.png)
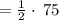

Therefore, area of the curve y= f(x) = x between x = 5 and x = 10