Question

A person walks first at a constant speed of 2 m/s along a straight line from point A to point B and then back along the line from B to A at a constant speed of 4 m/s. What is the average speed (in m/s) over the entire trip?

Answer 1

The average speed is 2.67 m/s

Step-by-step explanation:

Constant Speed Motion

The speed of a moving object can be calculated as:

`\displaystyle v=(x)/(t)`

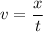
Where

x = distance

t = time

Solving for t:

`\displaystyle t=(x)/(v)`

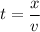
The average speed is calculated as:

`\displaystyle \bar v=(x_t)/(t_t)`

Where xt and tt are the total distance and time respectively.

The person walks at a constant speed of v1=2 m/s for a distance x. They take a time t1 to travel calculated by:

`\displaystyle t_1=(x)/(v_1)`

Then, the person walks back at v2=4 m/s the same distance x. Thus, the second time is:

`\displaystyle t_2=(x)/(v_2)`

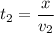
The total time taken for the entire travel is:

`\displaystyle t_t=(x)/(v_1)+(x)/(v_2)`

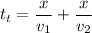
Simplifying and substituting:

`\displaystyle t_t=(x)/(2)+(x)/(4)`

`\displaystyle t_t=(2x)/(4)+(x)/(4)`

`\displaystyle t_t=(3x)/(4)`

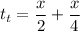
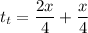
The total distance is xt=2x, thus the average speed is:

`\displaystyle \bar v=(2x)/((3x)/(4))`

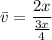
Simplifying:

`\displaystyle \bar v=(8)/(3)=2.67`

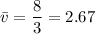
The average speed is 2.67 m/s