Question

HELPPPPPPPPPPPP!!! PLEASEEEEEE!! I NEED THIS RIGHT NOWWWW

Answer 1

h = 15.13 cm

Explanation:

Lateral Surface Area of a Cone

Given a right circular cone of base radius r and height h, the lateral surface area is given by:

`A=\pi r√(r^2+h^2)`

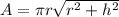
We are given the lateral area of a funnel as A=236.64 square cm and the radius is r=4.75 cm. It's required to find the height of the cone. It can be calculated by solving for h.

Squaring:

`A^2=\pi^2 r^2(r^2+h^2)`

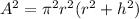
Dividing by
`\pi r^2`

`\displaystyle (A^2)/(\pi^2 r^2)=r^2+h^2`

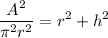
Subtracting
`r^2`:

`\displaystyle (A^2)/(\pi^2 r^2)-r^2=h^2`

Taking square root:

`\displaystyle h=\sqrt{ (A^2)/(\pi^2 r^2)-r^2}`

Substituting the values:

`\displaystyle h=√( 251.472-22.5625)`

`\displaystyle h=√( 228.909)`

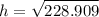
h = 15.13 cm