Question

PLEASEEEE HELPPPPPP!

Answer 1

We conclude that the value of 'a' will be:

`a=(x+b^2)/(2)`

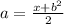
Hence, option (2) is true.

Explanation:

Given the equation

x = 2a - b²

Let us solve the equation to solve for 'a'

`x=2a-b^2`

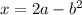
switching sides

`2a-b^2=x`

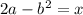
Add b² to both sides

`2a-b^2+b^2=x+b^2`

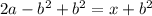
Simplify

`2a=x+b^2`

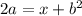
Divide both sides by 2

`(2a)/(2)=(x)/(2)+(b^2)/(2)`

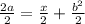
Simplify

`a=(x+b^2)/(2)`

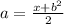
Therefore, we conclude that the value of 'a' will be:

`a=(x+b^2)/(2)`

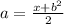
Hence, option (2) is true.