Answer:
Rs 20000
Explanation:
Let the sum is x.
The rate of interest, r=20%=0.2
Time, t=2 years.
Total amount after t years,
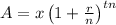
The value of n when compounded annually, n=1
So, the total amount,
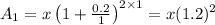
The compound interest when compounded annually,
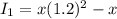
The value of n when compounded semi-annually, n=2
So, the total amount,
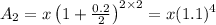
The compound interest when compounded semi-annually,
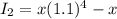
As the difference between the annual and semi-annual compound interest on x amount of money is Rs 482, so
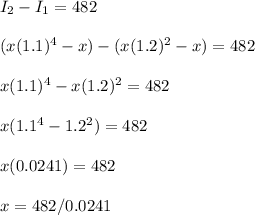
x=20000
Hence, the sum is Rs 20000.