Question

A constant horizontal F force began to act on the initially immovable body placed on a horizontal surface. After t time the force ceased to act, and after time 3t from the start of the movement the body stopped. Find the coefficient of friction between the body and the surface if the body mass is m.​

Answer 1

The coefficient of friction is (F/(19.6·m)

Step-by-step explanation:

The given parameters are;

The force applied to the immovable body = F

The time duration the force acts = t

The time the body spends in motion = 3·t

The acceleration due to gravity, g = 9.8 m/s²

From Newton's second law of motion, we have;

The impulse of the force = F × t = m × Δv₁

Where;

Δv₁ = v₁ - 0 = v₁

The impulse applied by the force of friction,
`F_f` is
`F_f` × (3·t - t) =
`F_f` × (2·t)

Given that the motion of the object is stopped by the frictional force, we have;

The impulse due to the frictional force = Momentum change = m × Δv₂ =
`F_f` × (2·t)

Where;

Δv₂ = v₂ - 0 = v₂

Given that the velocity, v₂, at the start of the deceleration = The velocity at the point the force ceased to act, v₁, we have;

m × Δv₂ =
`F_f` × (2·t) = m × Δv₁ = F × t

∴
`F_f` × (2·t) = F × t

`F_f` = F × t/(2·t) = F/2

The coefficient of dynamic friction,
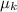`\mu _k` = Frictional force/(The weight of the body) = (F/2)/(9.8 × m)

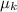`\mu _k` = (F/(19.6·m)

The coefficient of friction,
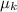`\mu _k` = (F/(19.6·m)