Question

Find the values of x in [0, 360°) which satisfy the
equation below.
2 cota x = -3 SC X

Answer 1

Given :

An equation 2cot x = -3sec x .

To Find :

the values of x in [0, 360°) which satisfy the given equation.

Solution :

Converting cot x and sec x in the form of sin x and cos x.

`(2cos \ x)/(sin\ x)= (-3)/(cosx)\\\\2cos^2 x +3 sin\ x =0\\\\2( 1 - sin^2 x ) + 3sin \ x = 0 \\\\2sin^2 x -3sin\ x -2 = 0\\\\2sin^2\x -4sin\ x + sin\ x -2 = 0\\\\2sin\ x( sin\ x - 2 )+ 1( sin \ x - 2 ) = 0\\\\sin \ x = (-1)/(2) \ or\ sin \ x = 2`

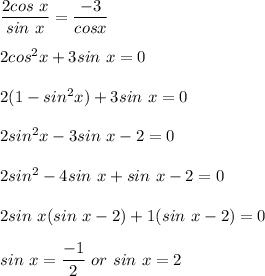
Neglecting sin x = 2 because sin x cannot be greater than 1.

x = π - π/6, π + π/6

x = 5π/6 and x = 7π /6

Therefore, the values of x in [0,360°) is 5π/6 and x = 7π /6 .