Answer:
a = 1
Explanation:
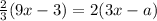
One must simplify this expression, by distributing. In order to find a solution, where x has infinite solutions, one must make this equation an identity. That means that the equation will hold true, no matter what value of x is plugged in.
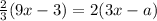
Distribute;
6x - 2 = 6x - 2a
Inverse operations;
6x - 2 = 6x - 2a
-6x -6x
-2 = -2a
1 = a
For this equation to be true no matter what, a must equal 1.