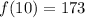Answer:
Explanation:
Given
Exponential Function
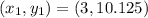
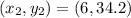
Required
Determine f(10)
We have that
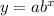
First, we need to solve for the values of a and b
For
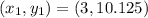
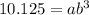 --- (1)
--- (1)
For
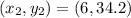
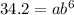 ---- (2)
---- (2)
Divide (2) by (1)
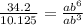
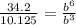

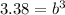
Take cube root of both sides
![b = \sqrt[3]{3.38}](https://img.qammunity.org/2021/formulas/mathematics/college/lxcqfrlhwlb5z4vj7hyotofx5sitk0akbr.png)
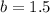
Substitute 1.5 for b in
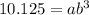

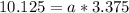
Solve for a
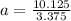

To solve for f(10).
This implies that x = 10
So, we have:
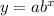 which becomes
which becomes
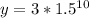
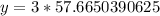
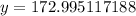
 -- approximated
-- approximated
Hence: