Question

Find the exact value of sec 330° in simplest form with a rational denominator.

Answer 1

`\implies \sec 330^o = (2)/(\sqrt3)=(2√(3))/(3)`

Explanation:

Given :-

• 
  `\sec 330^o`

And we need to find out its value . Firstly we know that 330° lies in 4th quadrant . And In fourth quadrant , cosine and secant are positive . Therefore , the result will be positive. Now we know that ,

`\implies \sec (360^o-\theta)= \sec\theta`

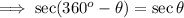
Using this ,

`\implies \sec (330^o) \\\\\rm\implies sec(360^o-30^o) \\\\\rm\implies \sec 30^o`

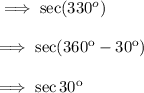
And the value of sec 30° is ,

`\implies \sec 30^o = (2)/(\sqrt3)`

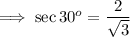
And by question we need to write it with a rational denominator .So on rationalising the denominator , we have ,

`\implies \sec 30^o = (2)/(\sqrt3)=\boxed{\red{(2\sqrt3)/(3)}}`

Hence the required answer is 2√3/3.

Answer 2

2√3/3

Explanation:

Sec(330°)

=1/cos(330°)

=1/√3/2 (since Cos (330°)=√3/2

=1×2/√3

=2/√3×√3/√3

=2√3/3