Question

Zan has created this rule for generating sequences of whole numbers. If a number is 25 or less, double the number. If a number is more than 25, subtract 12 from it. For example, if Zan starts with 10, she gets the sequence 10, 20, 40, 28, 16,... If the third number in Zan's sequence is 36, what is the sum of the four distinct numbers that could have been the first number in her sequence

Answer 1

123

Explanation:

Given that:

Method to generate the sequence:

If a number is less than or equal to 25, then the number is doubled.

And if the number is more than 25, then 12 is subtracted from it.

Here, we are given a sequence with its third number is 36.

Now, let us have a look by making the number 36 as half of its value.

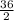`(36)/(2)` = 18

This could have been the second number in the.

According to this, the first number will be
`(18)/(2) = \bold{9}`

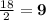
Other option for the first term can be 18 + 12 = 30

By second method, the second method can be:

36 + 12 = 48

By this method, First number 48 + 12 = 60

Other option for first number can be
`(48)/(2 ) = \bold{24}`

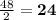
Therefore, sum of four options of first term:

9 + 30 + 60 + 24 = 123