Which expression is equivalent i^233? On edge

Question

asked Jun 13, 2021 66.9k views

1 Answer

Hafiz Temuri · Answer 1 · 2021-06-19T13:29:45+0000

Answer:

C

Explanation:

Remember the four basic power of i:

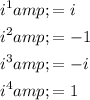
$\begin{aligned}i^1&=i\\i^2&=-1\\i^3&=-i\\i^4&=1\end{aligned}$

We have:

i^(233)

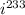
The trick here is to split the exponent into a number divisible by 4 plus the remainder. Notice that:

233=232+1

And that:

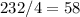
232/4=58

So, we can rewrite our exponent as:

$=i^{4\cdot 58+1$

Using the properties of exponents:

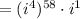
$=(i^4)^(58)\cdot i^1$

Since i to the fourth is simply 1:

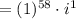
$=(1)^(58)\cdot i^1$

Simplify:

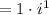
$=1\cdot i^1$

Simplify:

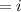
Hence, our answer is C.