Question

A group of 24 people need transportation from a hotel to a concert. They will be picked up by Uber drivers that can fit 4 passengers in their compact car and 6 passengers in their SUV’s. You would like to determine how many compact cars and SUVs could be used to transport the entire group. Let x = the number of compact cars and let y = the number of SUV's.

Write and graph an equation that models the situation.

Answer 1

Explanation:

Compact cars:

24 divided by 4 = 6

6 cars for 24 people

SUV's:

24 divided by 6 = 4

4 SUV's for 24 people

Answer 2

`4x+6y=24`

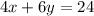
See below for graph.

Explanation:

A total of 24 people need to be transported.

Let x represent the number of Uber compact cars.

And let y represent the number of SUVs.

So, the number of people that can be picked up by x compact cars is 4x.

And the number of people that can be picked up by y SUVs is 6y.

And the total is 24 people. So, the two terms must total 24. So, we can write:

`4x+6y=24`

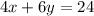
We can convert this to slope-intercept form. First, we can divide everything by 2:

`2x+3y=12`

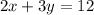
Subtracting 2x from both sides yields:

`3x=-2x+12`

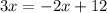
Finally, dividing both sides by 3 yields our linear equation:

`\displaystyle y=-(2)/(3)x+4`

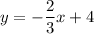
Please refer to the below attachment for the graph.

*Note that we should restrain our graph to only QI. This is because we cannot use negative compact cars of SUVs. Also, only integer points on the line will work, as we cannot have, say, 2.5 compact cars.

**Also, the x- and y-intercepts tell us the maximum of each type needed. Either we need 6 compact cars and 0 SUVs, (6, 0); 4 SUVs and 0 compact cars (0, 4); or a combination of them.