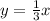Answer:
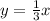
Explanation:
Perpendicular lines
Perpendicular lines have slopes whose product is -1. In other words, to find a line that is perpendicular to a given line, the new line must have a that is the opposite reciprocal of the original line.
Passing through a point
Additionally, if a line contains a point, then the point must be a solution to the equation (meaning, when you plug in the "x" and "y", the equation must be true).
Finding our perpendicular line
Work on slope first
To find the slope of the original line, rewrite the original line in slope-intercept form:

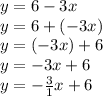
In this form, the slope is the number multiplied to the "x", so the original slope is -3/1.
Thus, the slope of the new perpendicular line will be the opposite reciprocal of -3/1 ... which is 1/3.
Writing what we do know about the new perpendicular line, we have
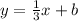
Making sure it passes through the point
This new line is also supposed to contain the point (-3,-1), so (-3,-1) must be a solution to the equation, for whatever constant-value the "b" is. To find out the "b", substitute the known quantities, and solve:
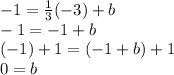
Substituting this into our equation:
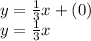
Conclusion
So, the equation for a line that is perpendicular to the original line
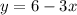 , and that also passes through (-3,-1) is
, and that also passes through (-3,-1) is