Answer:
The slope of the line passing through the points (−3, −5) and (−1, −6) is
 (-0.5)
(-0.5)
Explanation:
Equation of a straight line:
y = mx + b where m is the slope and b is the y-intercept
(x1, x2) and (y1, y2) : (−3, −5) and (−1, −6)
Calculating Slope (m).
m =
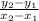
m =

m =
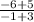
m =

we can take this a step further by finding the equation:
Now putting value of m in equation (i)
y = -0.5x + b
Calculating Y-intercept (b).
Lets choose the first point, (-3,-5) for calculating y-intercept:
y = mx + b
-5 = -0.5(-3) + b
-5 = 1.5 + b
-6.5 = b
b = -6.5
Now putting value of b in equation
y = -0.5x + -6.5