Question

Alice and Bob are experimenting with two moles of neon, a monatomic gas, that starts out at conditions of standard temperature and pressure (273.15 K, 105 Pa). Alice heats the gas at constant volume until its pressure is doubled, then Bob further heats the gas at constant pressure until its volume is doubled. If Alice and Bob assume that neon behaves as an ideal gas, then how much heat have they added to the gas for the entire process.

Answer 1

29273.178 joules have been added to the gas for the entire process.

Step-by-step explanation:

The specific heats of monoatomic gases, measured in joules per mol-Kelvin, are represented by the following expressions:

Isochoric (Constant volume)

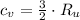`c_(v) = (3)/(2)\cdot R_(u)` (1)

Isobaric (Constant pressure)

`c_(p) = (5)/(2)\cdot R_(u)` (2)

Where
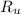`R_(u)` is the ideal gas constant, measured in pascal-cubic meters per mol-Kelvin.

Under the assumption of ideal gas, we notice the following relationships:

1) Temperature is directly proportional to pressure.

2) Temperature is directly proportional to volume.

Now we proceed to find all required temperatures below:

(i) Alice heats the gas at constant volume until its pressure is doubled:

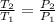`(T_(2))/(T_(1)) = (P_(2))/(P_(1))` (3)

(
`(P_(2))/(P_(1)) = 2`,
`T_(1) = 273.15\,K`)

`T_(2) = (P_(2))/(P_(1)) * T_(1)`

`T_(2) = 2* 273.15\,K`

`T_(2) = 546.3\,K`

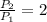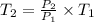
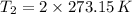
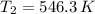
(ii) Bob further heats the gas at constant pressure until its volume is doubled:

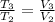`(T_(3))/(T_(2)) =(V_(3))/(V_(2))` (4)

(
`(V_(3))/(V_(2)) = 2`,
`T_(2) = 546.3\,K`)

`T_(3) = (V_(3))/(V_(2))* T_(2)`

`T_(3) = 2* 546.3\,K`

`T_(3) = 1092.6\,K`

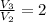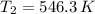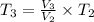
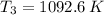
Finally, the heat added to the gas (
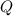`Q`), measured in joules, for the entire process is:

`Q = n\cdot [c_(v)\cdot (T_(2)-T_(1))+c_(p)\cdot (T_(3)-T_(2))]` (5)

If we know that
`R_(u) = 8.314\,(Pa\cdot m^(3))/(mol\cdot K)`,
`n = 2\,mol`,
`T_(1) = 273.15\,K`,
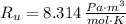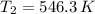`T_(2) = 546.3\,K` and
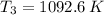`T_(3) = 1092.6\,K`, the heat added to the gas for the entire process is:

`c_(v) = (3)/(2)\cdot \left(8.314\,(Pa\cdot m^(3))/(mol\cdot K) \right)`

`c_(v) = 12.471\,(J)/(mol\cdot K)`

`c_(p) = (5)/(2)\cdot \left(8.314\,(Pa\cdot m^(3))/(mol\cdot K) \right)`

`c_(p) = 20.785\,(J)/(mol\cdot K)`

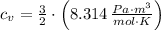
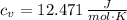
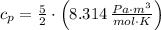
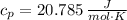
`Q = (2\,mol)\cdot \left[\left(12.471\,(J)/(mol\cdot K) \right)\cdot (536.3\,K-273.15\,K)+\left(20.785\,(J)/(mol\cdot K) \right)\cdot (1092.6\,K-546.3\,K )\right]`

`Q = 29273.178\,J`

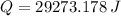
29273.178 joules have been added to the gas for the entire process.