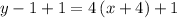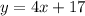Write an equation in point-slope form of the line that passes through the given point and with the given slope m. (-4,1) m=4 The equation of the line is ?

Question

asked Jul 17, 2021 113k views

1 Answer

Augusto Carmo · Answer 1 · 2021-07-21T11:31:38+0000

Answer:

An equation in point-slope form of the line that passes through the given point and with the given slope m = 4 will be:

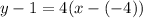
y-1 = 4(x-(-4))

Explanation:

Given

Using the point-slope form of the line equation

$y-y_1=m\left(x-x_1\right)$

here:

substituting the values m = 4 and the point (-4, 1) in the point-slope form of the line equation

$y-y_1=m\left(x-x_1\right)$

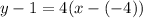
y-1 = 4(x-(-4))

Thus,

An equation in point-slope form of the line that passes through the given point and with the given slope m = 4 will be:

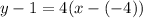
y-1 = 4(x-(-4))

Note: It can further be simplified

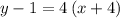
$y-1=4\left(x+4\right)$

Add 1 to both sides

$y-1+1=4\left(x+4\right)+1$

y=4x+17