Question

Let n1=50​, X1=10​, n2=50​, and X2=30. Complete parts​ (a) and​ (b) below. a. At the 0.10 level of​ significance, is there evidence of a significant difference between the two population​ proportions? Determine the null and alternative hypotheses. Choose the correct answer below. A. H0: π1≤π2 H1: π1>π2 B. H0: π1≠π2 H1: π1=π2 C. H0: π1≥π2 H1: π1<π2 D. H0: π1=π2 H1: π1≠π2 Your answer is correct. Calculate the test​ statistic, ZSTAT​, based on the difference p1−p2. The test​ statistic, ZSTAT​, is nothing.

Answer 1

|Z| = |-4.089| > 1.645 at 0.10 level of significance

Null hypothesis is rejected at 0.10 level of significance

There is a difference between the two Population proportions

Explanation:

Step(i):-

Given first sample size (n₁) = 50

Given proportion of the first sample p⁻₁= 0.2

Given second sample size (n₂) = 50

Given proportion of the second sample p₂⁻ = 30/50 = 0.6

Null Hypothesis : H₀: p₁⁻=p₂⁻

Alternative Hypothesis : H₁: p₁⁻≠p₂⁻

Step(ii):-

Z-statistic

`Z = \frac{p_(1) -p_(2) }{\sqrt{pq((1)/(n_(1) ) +(1)/(n_(2)) ) } }`

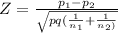
Where

`P = (n_(1)p_(1) +n_(2) p_(2) )/(n_(1) +n_(2) )`

`P = (50X0.2+50X0.6)/(50+50) = 0.4`

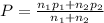
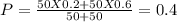
Z-statistic

`Z = \frac{0.2-0.6}{\sqrt{0.4 X 0.6((1)/(50)+(1)/(50) } }`

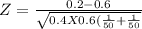
Z = -4.089

Level of significance =0.10

Z₀.₁₀ = 1.645

|Z| = |-4.089| > 1.645 at 0.10 level of significance

Null hypothesis is rejected at 0.10 level of significance

Final answer:-

There is a difference between the two Population proportions