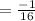Question

A player chooses one of the numbers 1 through 4. After the choice has been made, two regular four-sided (tetrahedral) dice are rolled, with the sides of the dice numbered 1 through 4. If the number chosen appears on the bottom of exactly one die after it is rolled, then the player wins If the number chosen appears on the bottom of both of the dice, then the player wins If the number chosen does not appear on the bottom of either of the dice, the player loses What is the expected return to the player, in dollars, for one roll of the dice

Answer 1

Answer:
`=(-1)/(16)`

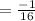
Explanation:

given data:

number to be chosen from = 1,2,3,4.

Solution:

ways the number can show

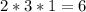`2*3*1=6` ways for your number to appear once.

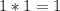`1*1=1` ways for your number to appear twice.

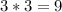`3*3=9` ways for your number not to appear at all

`= (6(1) + 1(2) - 9(1))/(16)`

`= (6+2-9)/(16)`

`=(-1)/(16)`

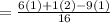
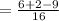
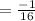
expected return of the player is
`=(-1)/(16)`