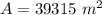Answer:
The value is
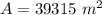
Step-by-step explanation:
From the question we are told that
The velocity which the rover is suppose to land with is
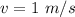
The mass of the rover and the parachute is
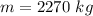
The drag coefficient is
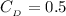
The atmospheric density of Earth is
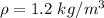
The acceleration due to gravity in Mars is

Generally the Mars atmosphere density is mathematically represented as
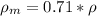
=>
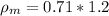
=>
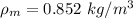
Generally the drag force on the rover and the parachute is mathematically represented as
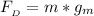
=>
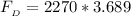
=>
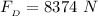
Gnerally this drag force is mathematically represented as
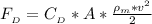
Here A is the frontal area
So
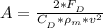
=>
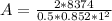
=>