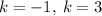Question

If (x+2) is a factor of 3x^2-4kx-4k^2, then find the value(s) of k

Answer 1

The values of k will be:

`k=-1,\:k=3`

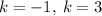
Explanation:

Let the expression of polynomial P be

`P\left(x\right)=3x^2-4kx-4k^2`

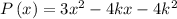
Let the expression if the polynomial Q be

`\:Q\left(x\right)=\:\left(x+2\right)\:`

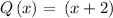
Plug in Q(x) = 0

0 = x+2

x = -2

As (x+2) is a factor of 3x²-4kx-4k²

substitute x = -2 in the the polynomial

3x²-4kx-4k² = 0

`3\left(-2\right)^2-4k\left(-2\right)-4k^2\:=0`

`12+8k-4k^2=0`

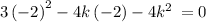
Write in the standard form ax²+bx+c = 0

`-4k^2+8k+12=0`

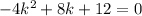
Factor out common term -4

`-4\left(k^2-2k-3\right)=0`

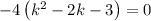
Factor k²-2k-3: (k+1)(k-3)

`-4\left(k+1\right)\left(k-3\right)=0`

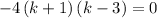
Using the zero factor principle

if ab=0, then a=0 or b=0 (or both a=0 and b=0)

`k+1=0\quad \mathrm{or}\quad \:k-3=0`

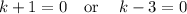
solving k+1=0

k+1 = 0

k = -1

solving k-3=0

k-3=0

k = 3

Thus, the values of k will be:

`k=-1,\:k=3`