Question

One - step adding/ subtraction equation / multiplication/ division problems

The height of the water in an above ground pool is 36 inches. The pool needs to be drained. As the water drains, the height of the water changes at a rate of -1/2 inch per minute. Write and solve and equation to find out how many minutes it will take to drain the pool.

Answer 1

It would take x = 72 minutes to drain the pool.

Explanation:

We know that the slope-intercept form of the line equation is

`y = mx+b`

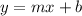
where m is the rate of change or slope and b is the y-intercept

• Let 'y' be the height of the water pool

• Let 'x' be the time in the minute of the water pool

As the height of the water of the pool is 36 inches, meaning the basic condition of the pool states that the ground pool is 36 inches.

Thus,

• y-intercept = b = 36

As the water drains, the height of the water changes at a rate of -1/2 inch per minute.

• Thus, the rate of change or slope = m = -1/2

Thus, using the equation

`y = mx+b`

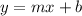
substituting m = -1/2 and b = 36

`y\:=\:-(1)/(2)x+36`

We know that when the pool drains, the height of water reduces to zero.

Thus, substituting y = 0 in the equation

`0=-(1)/(2)x+36`

switching sides

`-(1)/(2)x+36=0`

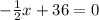
subtract 36 from both sides

`-(1)/(2)x+36-36=0-36`

`-(1)/(2)x=-36`

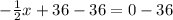
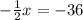
Multiplying both sides by -2

`\left(-(1)/(2)x\right)\left(-2\right)=\left(-36\right)\left(-2\right)`

`x=72`

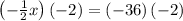
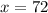
Therefore, it would take x = 72 minutes to drain the pool.