Answer:
The rate of change is -4.5 and the relation of the table is a linear function
Explanation:
Linear function.
A linear function can be identified because the rate of change is constant at every point of its domain.
The graph of a linear function is a straight line with a constant slope.
Suppose we know the line passes through points A(x1,y1) and B(x2,y2). The slope can be calculated with the equation:
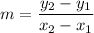
We'll show the relation shown in the table is a linear function. We'll calculate the slope for any random pair of points. For example, using (2,83) and (3,78.5):
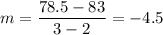
Now for (7,60.5) and (14,29):
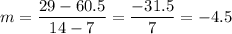
Proceeding in a similar way with any pair of points, the slope will always result in the same value, thus the rate of change is -4.5 and the relation of the table is a linear function.