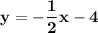Question

What is an equation in slope-intercept form of the line that passes through (6, −7) and is perpendicular to the line shown below?

Answer 1

A.
`\displaystyle y = -(1)/(2) x -4`

Explanation:

Equation of a Line

The equation of the line in slope-intercept form is:

y=mx+b

Where:

m = slope

b = y-intercept.

The point-slope form of the equation of a line is:

y - k = m ( x - h )

Where:

(h,k) is a point through which the line passes.

The line we are looking for has a slope defined for the fact that is perpendicular to the line shown in the graph.

Two perpendicular lines with slopes m1 and m2 satisfy the equation:

`m_1m_2=-1`

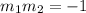
We'll find the slope m1 of the given line and then solve the above equation for m2:

`\displaystyle m_2=-(1)/(m_1)`

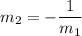
The line of the graph passes through two clear points (-3,-3) and (0,3). Let's calculate the slope.

Suppose we know the line passes through points A(x1,y1) and B(x2,y2). The slope can be calculated with the equation:

`\displaystyle m_1=(3+3)/(0+3)=(6)/(3)=2`

Now we calculate the second slope:

`\displaystyle m_2=-(1)/(2)`

We use the point-slope form, given the point (6,-7):

`\displaystyle y + 7 = -(1)/(2) ( x - 6 )`

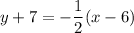
Operating the parentheses:

`\displaystyle y + 7 = -(1)/(2) x +(1)/(2)\cdot 6 )`

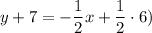
Simplifying:

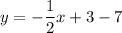
`\displaystyle y = -(1)/(2) x +3-7`

A.
`\mathbf{\displaystyle y = -(1)/(2) x -4}`