Question

Write two expressions with unlike denominators whose sum is x-3/x+2, I need help it is confusing for me.

Answer 1

`\displaystyle A=(x-2)/(x+3)`

`\displaystyle B=(-5)/((x+3)(x+2))`

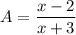
Explanation:

We need to find two expressions with unlike denominators what sum

`\displaystyle S=(x-3)/(x+2)`

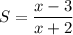
Let's suppose one of the expressions is:

`\displaystyle A=(x-2)/(x+3)`

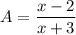
Now we subtract S minus A to find the other expression B:

`\displaystyle B=S-A=(x-3)/(x+2)-(x-2)/(x+3)`

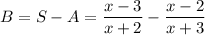
Multiply the first fraction by x+3 and the second by x+2;

`\displaystyle B=(x+3)(x-3)/((x+3)(x+2))-(x+2)(x-2)/((x+3)(x+2))`

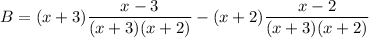
Operating:

`\displaystyle B=(x^2-9)/((x+3)(x+2))-(x^2-4)/((x+3)(x+2))`

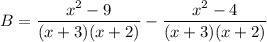
Subtracting both fractions with like denominators:

`\displaystyle B=(x^2-9-(x^2-4))/((x+3)(x+2))`

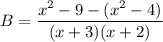
Simplifying:

`\displaystyle B=(-5)/((x+3)(x+2))`

Thus the two expressions are:

`\displaystyle A=(x-2)/(x+3)`

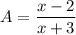
And

`\displaystyle B=(-5)/((x+3)(x+2))`