Question

Let p (x ) = x^3 - 3x^2 - 10x + 24. What is the remainder when p (x ) is divided by x - 1?

Answer 1

The remainder is 12.

Explanation:

The Polynomial Remainder Theorem

The remainder of the division of a polynomial f(x) by (x-a) is equal to f(a).

We are given the polynomial:

`p (x ) = x^3 - 3x^2 - 10x + 24`

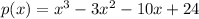
And we are required to find the remainder when p(x) is divided by (x-1).

We can simply apply the polynomial remainder theorem, substituting x for 1 in the polynomial:

`Remainder=p (1 ) = 1^3 - 3\cdot 1^2 - 10(1) + 24`

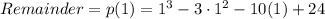
Remainder= 1 - 3 - 10 + 24 = 12

The remainder is 12.