X^a=y^b=z^c \\xyz=1\\ab+bc+ca=?

Question

asked Jan 19, 2021 103k views

1 Answer

Richard Birkett · Answer 1 · 2021-01-24T08:38:06+0000

Answer:

ab+bc+ca=0

Explanation:

We are given:

x^a=y^b=z^c

xyz=1

Separating equations:

x^a=z^c

y^b=z^c

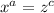
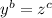
Solving the first equation for x:

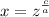
$\displaystyle x=z^(c)/(a)$

Solving the second equation for y:

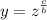
$\displaystyle y=z^(c)/(b)$

Substituting in

xyz=1:

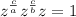
$\displaystyle z^(c)/(a)z^(c)/(b)z=1$

Adding the exponents:

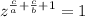
$\displaystyle z^{(c)/(a)+(c)/(b)+1}=1$

Since
1=z^0 :

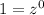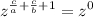
$\displaystyle z^{(c)/(a)+(c)/(b)+1}=z^0$

The base is z on both sides so we get rid of them:

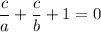
$\displaystyle (c)/(a)+(c)/(b)+1=0$

Multiplying by ab:

bc+ac+ab=0

Reordering:

ab+bc+ca=0