The sled accelerates with magnitude
 such that
such that
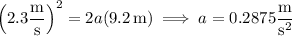
By Newton's second law, the net force in the plane of motion (parallel to the ground) is
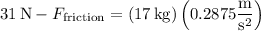
so that the force of friction exerts a magnitude of
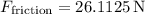
Perpendicular to the ground, the sled is in equilibrium, so Newton's second law says

The magnitude of friction is proportional to the magnitude of the normal force by a factor of
 , the coefficient of kinetic friction. It follows that
, the coefficient of kinetic friction. It follows that

(and the coefficient is dimensionless).