Question

Anyone....................​

Answer 1

`h_1 = 18 \: cm`

Step-by-step explanation:

See image for explanation

I hope my working is correct.

Answer 2

h₁ = 18 [cm]

Step-by-step explanation:

This problem can be solved by applying the principles of the static pressure of a liquid column. The key to the solution is to know that the pressure on the horizontal line should be equal for both liquids, this must be met regardless of their density.

`P_(2)=P_(1)\\`

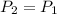
where:

P₂ = Pressure exerted by the liquid 2 in the given point L₂

P₁ = Pressure exerted by the liquid 2 in the given point L₁

Now we can calculate the pressure in each point using the following expression:

`P_(1)=Ro_(1)*g*h_(1)\\P_(2)=Ro_(2)*g*h_(2)`

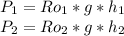
Where:

Ro₁ = density of the liquid 1 = 0.8 [g/cm³]

Ro₂ = density of the liquid 2 = 1.8 [g/cm³]

g = gravity acceleration = 9.81 [m/s²]

h₁ = column of the liquid 1 [m]

h₂ = column of the liquid 2, = 8 [cm] = 0.08 [m]

But first we must convert the units from grams per cubic centimeter to kilograms per cubic meter.

`0.8[(g)/(cm^(3))]*[(1kg)/(1000g) ]*[(100^(3)cm^(3) )/(1m^(3) ) ]=800[kg/m^(3) ]\\1.8[(g)/(cm^(3))]*[(1kg)/(1000g) ]*[(100^(3)cm^(3) )/(1m^(3) ) ]=1800[kg/m^(3) ]`

Now replacing in the first equation:

`800*9.81*h_(1)=1800*9.81*0.08\\h_(1)=(1800)/(800) *0.08\\h_(1)=0.18 [m] = 18 [cm]`