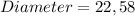Question

Find the diameter of a circle if its area is

a. 100cm2
Ibucm2
c. 400mcm2
d. - ncm2
4​

Answer 1

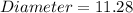`Diameter = 11.28`cm --- (a)

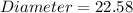`Diameter =22.58` cm --- (c)

Explanation:

Only (a) & (c) are clear enough to be solved. Others are not properly presented.

Use the following explanations of (a) & (c) to answer others.

`a.\ Area = 100cm^2`

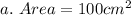
Area is calculated as:

`Area = \pi r^2`

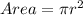
Substitute 100 for Area

`100 = \pi r^2`

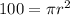
Take π as 3.14. So, the expression become

`100 = 3.14 r^2`

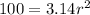
Divide both sides by 3.14

`(100)/(3.14) = (3.14 r^2)/(3.14)`

`(100)/(3.14) = r^2`

`r^2 = (100)/(3.14)`

`r^2 = 31.847133758`

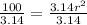
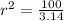
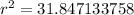
Solve for r

`r = \sqrt{31.847133758`

`r = 5.64`

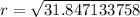
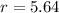
But diameter = 2 * radius

So:

`Diameter = 2 * 5.64`

`Diameter = 11.28`

`a.\ Area = 400cm^2`

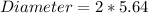
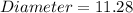
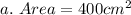
Area is calculated as:

`Area = \pi r^2`

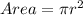
Substitute 400 for Area

`400 = \pi r^2`

`400 = 3.14 r^2`

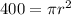
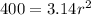
Divide both sides by 3.14

`(400)/(3.14) = (3.14 r^2)/(3.14)`

`(400)/(3.14) = r^2`

`r^2 = (100)/(3.14)`

`r^2 = 127.388535032`

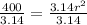
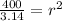
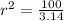
Solve for r

`r = \sqrt{127.388535032`

`r = 11.29`

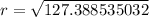
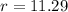
But diameter = 2 * radius

So:

`Diameter = 2 * 11.29`

`Diameter =22,58`