Answer:
The force of friction required to keep the car from sliding down the hill is 898.054 newtons and since
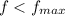 , the car will not slide down the hill.
, the car will not slide down the hill.
Step-by-step explanation:
The free body diagram is included below and now we prepare each equation of equilibrium for respective orthogonal axis:
 (1)
(1)
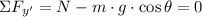 (2)
(2)
Where:
 - Static friction force, measured in newtons.
- Static friction force, measured in newtons.
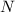 - Normal force from the inclined hill to the car, measured in newtons.
- Normal force from the inclined hill to the car, measured in newtons.
 - Mass of the car, measured in newtons.
- Mass of the car, measured in newtons.
 - Gravitational constant, measured in meters per square second.
- Gravitational constant, measured in meters per square second.
 - Angle of inclination of the hill, measured in sexagesimal degrees.
- Angle of inclination of the hill, measured in sexagesimal degrees.
If we know that
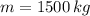 ,
,
 and
and
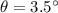 , then the friction force required to keep the car from sliding down the hill is:
, then the friction force required to keep the car from sliding down the hill is:
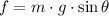
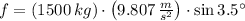

The force of friction required to keep the car from sliding down the hill is 898.054 newtons.
If the car does not slide down the hill, then the following condition must be observed:
 (2)
(2)
Where
 is the static coefficient of friction, dimensionless.
is the static coefficient of friction, dimensionless.
If we know that
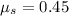 ,
,
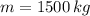 ,
,
 and
and
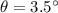 , then the maximum allowable static friction force is:
, then the maximum allowable static friction force is:
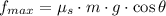
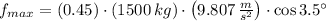
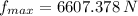
Since
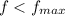 , the car will not slide down the hill.
, the car will not slide down the hill.